How Do Chess Engines Really Work?

Since 1997, with the victory of IBM's chess program Deep Blue against the reigning world champion Garry Kasparov, computers have clearly outclassed humans. Nowadays, top engines like Stockfish, 17 times winner of the Top Chess Engine Championship (TCEC), are able to achieve ELO ratings over 3500, making them unbeatable by any human. Chess programs are also omnipresent in training and game analysis. They generate all sorts of statistics to help us improve. In this context, it might be helpful to have a bit of understanding of the mechanisms at work in these algorithms. In this article, I'll explain how they work under the hood, and at the end, relate that with a Python chess engine project that I started recently.

The Basic Concepts

Let's now start by seeing the fundamental ideas which most if not all modern chess engines use.

The Evaluation Function

You may be familiar with Stockfish's evaluation function, which is displayed in analysis boards. An evaluation function has the goal to evaluate the "winning chances" or the "advantage" of a player. It is static, meaning it only analyzes the position itself, not sequences of possible moves. Most of the time, it is symmetric, with a negative score being an advantage for black, and a positive score being an advantage for white.
For the calculation, it generally adds up several factors, like:

• Material, with standard values associated to piece types
• Position, based on piece-square tables, which assign bonuses or penalties depending on piece type and square
• Mobility: number of legal moves in the position
• King safety, with e.g. penalties for attacks near the king
• Center control, with bonuses for the control of central squares
• Pawn structure: e.g. penalties for doubled, isolated or backward pawns and bonuses for passed pawns
• Etc...

Most engines vary weights associated with these factors depending on the phase of the game (opening, middlegame, or endgame).

Another (much more complex) approach to building an evaluation function is using NNUE, or Efficiently updatable neural network. The very basic idea behind is to train a neural network to assign a score to positions, effectively replacing a handcrafted evaluation function. It is quite recent, as Stockfish, the first engine to integrate it, did it in 2020! However, as of today, almost all the best programs have integrated it.

Minimax Search

Game Trees

For the moment, our evaluation function alone won't be able to play very well. The engine needs to see not only its move, but also the response of the opponent, its own move after that, and so on as far as possible. We generally model the possible sequences of moves with a game tree, like this one:

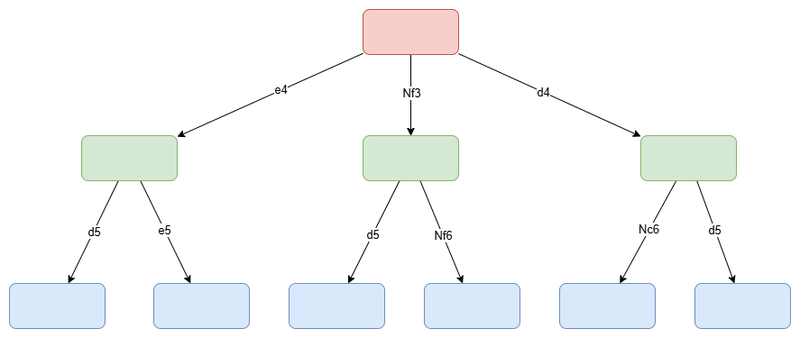
A simplified example game tree with moves chosen at random

(Note: In reality, the tree is much larger than that, with the average number of legal moves possible being approximately between 31 and 35)

Each node (box) represents a position, and each branch (arrow) a move. The topmost node is called the root, and the bottommost nodes are the leaves. The "distance" between the root and the leaves is called the depth, and it corresponds to the number of plies (half-turns) ahead that the engine considers. In this particular example, the depth is 2.

The Minimax Algorithm

The Minimax algorithm starts by evaluating the leaves, using the evaluation function. However, one very important thing is that the evaluation must be relative to the engine (root player). That concretely means that if the engine plays black, we will invert the sign of the values, so that the evaluation is relative to black. With our example, it could look like this:

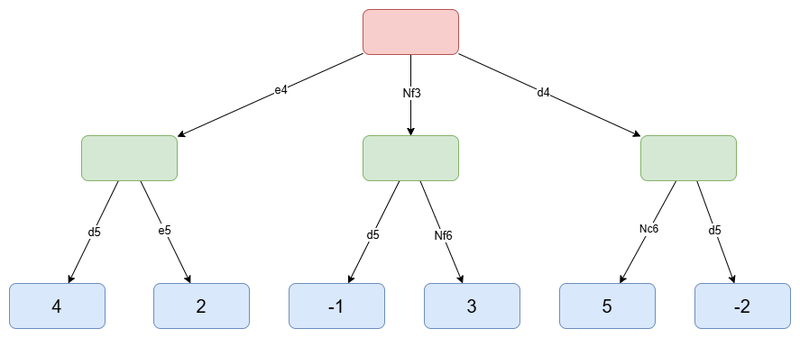
The same tree, with leaf nodes evaluated (the values are chosen arbitrarily)

Then, the algorithm works following that principle: you want to maximize your gains, while your opponent wants to minimize your gains. In this situation, you are called the maximizing player, and your opponent the minimizing player.

Concretely, that means we can evaluate backwards each node in the tree until we reach the root, applying the following rules:

• When it is the minimizing player's turn in a node, we assign to that node the minimum of the values of its child nodes
• When it is the maximizing player's turn in a node, we assign to that node the maximum of the values of its child nodes

Here is the result that would be obtained in our example:

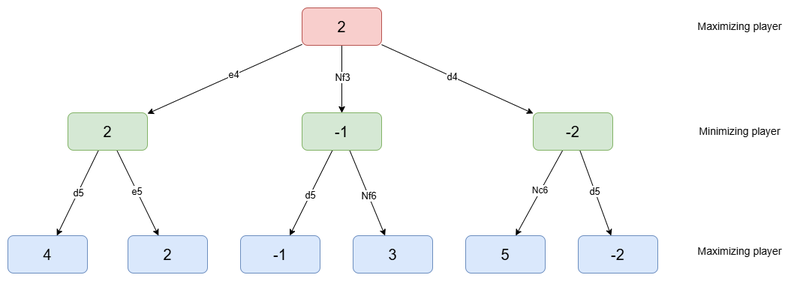
The result of the application of the Minimax algorithm to the tree

Finally, the best move is the one that guarantees the most points. In our example, the best move would be e4, with an evaluation of 2. That means that if both players play perfectly, after 2 plies, the evaluation function will show an advantage of 2 for the maximizing player.

(Just for information, there exists another algorithm called Negamax, which is simply another (quicker) way to transform the procedure described above into code. It yields exactly the same results as the Minimax implementation.)

Alpha-Beta Pruning

Raw Minimax search can get quite slow as the depth increases, because of the exponential growth of the number of nodes (positions) to visit. One very common way to improve speed and efficiency while keeping the same results is alpha-beta pruning.
As an example, consider the previous diagram again. Do you see any leaf which didn't need to be evaluated? If you look well, you'll notice it is the case for the 4th leaf from the left.

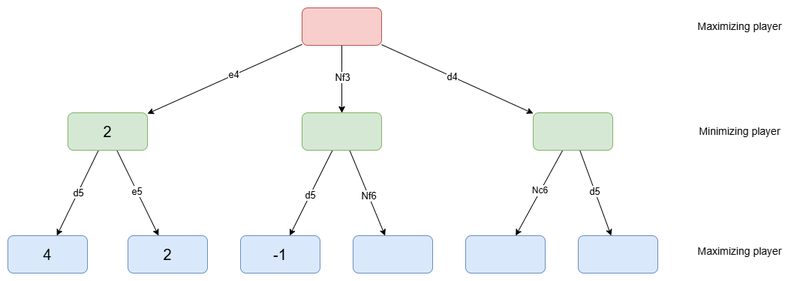
The state of the tree before the evaluation of the 4th leaf

In this situation, we know that whatever the evaluation of the 4th leaf is, the value of its parent node will be less or equal to -1 (as min(x, ?) ≤ x). But the first non-leaf node (the one after the move e4) was already evaluated and had a value of 2. That means that whatever the value of the 4th leaf is, Nf3 will be worse than e4, as 2 > -1. In consequence, the maximizing player will avoid Nf3, as there will always be a move better than that. Therefore, in this situation, we don't need to evaluate the next leaf — its value cannot change the outcome.

This example illustrates the core idea behind alpha-beta pruning. I find this concept a bit difficult to get a grasp on, so if you don't fully understand, don't worry. The general principle of it is just: if evaluating a node wouldn't affect the final result, don't bother evaluating it. Generally, it happens when a move is "too good" for either player, which means the other player would have avoided the situation.

More Advanced Improvements

Now that we have seen the basic logic used by chess engines, let's dive into more advanced improvements and optimization techniques that can be used to enhance the performance.

Quiescence Search

With pure Minimax search only, the engine stops searching at a fixed depth, which might for instance lead to inaccurate exchange evaluation. As an example, let's say we search at depth 2, and the last move examined is the capture of a rook. The engine will probably consider this as a good move, but if in reality the capture led to the loss of its queen on the move just after, it won't see it. This phenomenon is called the horizon effect, and it is one of the main issues with Minimax-only search.

The idea behind quiescence search is to evaluate further "tactical" moves: captures, checks, promotions... Non-tactical moves (also called quiet moves) aren't evaluated during this phase. With that extension, Minimax remains the main search algorithm, but a bit more time is spent searching deeper non-quiet moves. This allows the engine to avoid the horizon effect, thus improving the accuracy of the search.

Transposition Table

In chess, different sequences of moves might lead into the exact same position. Such sequences are called transpositions. In the case of our algorithm, this means that we may be evaluating the score associated to the same position several times! To solve that issue, we can use a transposition table, which stores the value calculated from each position previously encountered. That way, whenever we reach a position, we can check whether it has already been evaluated, and if that's the case, we look up for the score in the transposition table. (Generally, positions aren't stored as such, they are converted to integers using a method called Zobrist hashing.)

Move Ordering

Alpha-beta pruning generally cuts off more nodes when moves are considered from best to worst. We don't know exactly which move is the best before performing a full search, but we can try to guess it using several techniques. Here are the basic ideas it is built upon:

1. First Move

What can be done to find a good first (best) move is simply to use the move stored in the transposition table, if there is one. We will see another possibility in the next section (Iterative Deepening).

2. Capture Ordering

We need to be able to order capture moves, as some captures are better than others. For that, we can use MVV-LVA, which stands for Most Valuable Victim - Least Valuable Attacker. The idea is simply to advantage captures of an important piece with the least important piece. Even if this works, it is not the most accurate sorting technique. For full accuracy, capture ordering often uses Static Exchange Evaluation (often abbreviated SEE), which considers the full series of captures possible, thus evaluating the final material gain or loss.

3. Non-Capture Ordering

All the quiet (non-capture) moves also need to be ordered. For that, there are several possibilities, but I won't go into the details for them, as the article is already quite long. However, if you are curious, you can take a look at the Killer heuristic or the History heuristic.

Iterative Deepening

For the moment, the engine needs to choose a fixed depth to search at, and perform the Minimax algorithm at that depth. This behavior isn't great for time management, as we don't know how much time the search is going to take. In order to solve this problem, we can use iterative deepening. The principle is the following: we start by searching at depth 1, and then increment the depth until we reach the end of the time allocated. Then, the best move is just the move returned by the last fully completed search.
This process might seem to be a waste of time, as at each step, we are almost re-doing the previous search, just going one ply further. A compensation is that the values stored into the transposition table during the shallower searches can be reused for the deeper searches. It is also possible to retain the best move of the previous search first for the next search, improving move ordering, thus causing more alpha-beta cut-offs.

Chess Engine Design

One thing I did not mention is that some engines do not exactly follow the design described here. For example, Leela Chess Zero (Lc0) (another top-level engine) is almost entirely neural-based, still performing some search, but not using Minimax. Maia (an engine meant to play in a more human-like way), for its part, completely relies on a neural network.

One even more crucial point I did not talk about is that before coding this move search logic described here, you have to implement all of the basics of chess: the representation of the board, how pieces move, what is a check, a checkmate... This might seem as an obvious part, but in reality, it isn't so easy, and it is crucial, both for correctness and speed. Correctness is maybe the most important part, because we obviously want the engine to play only legal moves, even in edge cases (e.g. check within en passant). Speed, especially in move generation, has a very significant impact on the search depth that can be reached.

My Toy Chess Engine

Recently, I started writing a tiny chess engine in Python. I somewhat cheated concerning the last point described: for the "basis" (move generation) implementation, I used a ready-to-use library called python-chess. This allowed me to focus on the evaluation and search logic. I did a basic implementation similar to what I described above, and made the engine play on Lichess under the name @SomePythonBot. The bot is around 1700 to 1800 Elo at the moment, but this may vary in the future. Its level has nothing to do compared with top engines or grandmasters, but I think a slightly more optimized program, written in a faster language like C/C++ or Rust, could easily achieve 2000+ Elo. Still, if you want to find more details about the implementation, you can take a look at the repository containing the source code.

Conclusion

I hope my explanations were clear enough so you now know more about the main mechanisms at work inside chess engines. If you want to go further into the topic, you can explore the Chess Programming Wiki — a great resource that covers everything from basic concepts to very advanced ones. And, if you enjoy programming, I highly encourage you to try building your own chess engine. It's a challenging but fun process, as well as an opportunity to learn a lot.

Thank you for reading!